ラ・サール中学校 2005年 問題2の(2)
こんにちは。
昨夜メルマガを送らせていただいたのですが
どうも分数がズレて表示されるので
こちらにメインのところだけのせますね。
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
◆◆◆ 〔2〕メインコンテンツ
◆◆◆
◆◆◆ ラ・サール中学校 2005年2の(2)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
ちょっと今回から規則性の話になります。
まずは簡単な問題から。
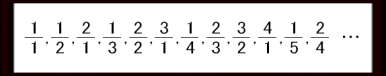
上のように規則的に数が並んでいます。値が1/2(2分の1)となる
4番目の数は前から数えて何番目の数でしょうか。
という問題です。
値が1/2ということですから、約分して1/2ということです。
つまり1/2, 2/4, 3/6, 4/8ということで
4番目の数は4/8です。約分出来ないとつらいですね。
これが前(はじめの数)から数えて何番目でしょうかという問題です。
パズルをやっていると数を数とだけではとらえないようになります。
かたまりでとらえようとしますね。
今回のはかたまりでとらえてもらわないと時間が足りなくなります。
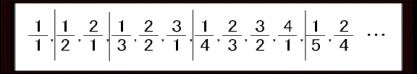
これで考えるとはじめに分母に8が出てくるのは
8個目のかたまりですが、そのときの分子は1になります。
ですからずらしていくと9個目で分子が2、
10個目で3、11個目で4となり8分の4、
つまり2分の1になります。
それでははじめから数えて何番目かという話ですが
10個目プラス4でいいことになりますよね。
10個目までの数というのは
1+2+3+4+・・・8+9+10と同じで
これはお馴染みのガウスの計算で
1 + 2+3+4+・・・8+9+10
10+ 9+8+7+・・・3+2+1 を足してすべて11になって
その11が10個だから110。
二つを足したのだから半分にして55。
それで元にもどって55+4=59(番目)ということになります。
このような思考が自然とできるようにパズル教材をつくって
低学年からパズルとして親しんでいきたいなって思ってます。
1,2分で解けるようになるとうれしいですね。
次回はもうちょっと難しいのにします。
11月号のマガジンには規則性の問題を入れる予定です。
それでは。
===================
以上です。
実際のメルマガはその前後に他のコンテンツがあります。
昨夜メルマガを送らせていただいたのですが
どうも分数がズレて表示されるので
こちらにメインのところだけのせますね。
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
◆◆◆ 〔2〕メインコンテンツ
◆◆◆
◆◆◆ ラ・サール中学校 2005年2の(2)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
ちょっと今回から規則性の話になります。
まずは簡単な問題から。
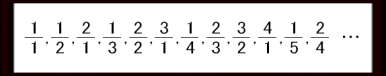
上のように規則的に数が並んでいます。値が1/2(2分の1)となる
4番目の数は前から数えて何番目の数でしょうか。
という問題です。
値が1/2ということですから、約分して1/2ということです。
つまり1/2, 2/4, 3/6, 4/8ということで
4番目の数は4/8です。約分出来ないとつらいですね。
これが前(はじめの数)から数えて何番目でしょうかという問題です。
パズルをやっていると数を数とだけではとらえないようになります。
かたまりでとらえようとしますね。
今回のはかたまりでとらえてもらわないと時間が足りなくなります。
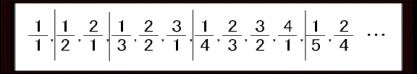
これで考えるとはじめに分母に8が出てくるのは
8個目のかたまりですが、そのときの分子は1になります。
ですからずらしていくと9個目で分子が2、
10個目で3、11個目で4となり8分の4、
つまり2分の1になります。
それでははじめから数えて何番目かという話ですが
10個目プラス4でいいことになりますよね。
10個目までの数というのは
1+2+3+4+・・・8+9+10と同じで
これはお馴染みのガウスの計算で
1 + 2+3+4+・・・8+9+10
10+ 9+8+7+・・・3+2+1 を足してすべて11になって
その11が10個だから110。
二つを足したのだから半分にして55。
それで元にもどって55+4=59(番目)ということになります。
このような思考が自然とできるようにパズル教材をつくって
低学年からパズルとして親しんでいきたいなって思ってます。
1,2分で解けるようになるとうれしいですね。
次回はもうちょっと難しいのにします。
11月号のマガジンには規則性の問題を入れる予定です。
それでは。
===================
以上です。
実際のメルマガはその前後に他のコンテンツがあります。

