先ほどのラ・サール2005年のちょっと違う解き方
先ほどの問題なのですが
もっとちょっと違うとらえ方も出来ます。
もう一度、問題を書きますね。
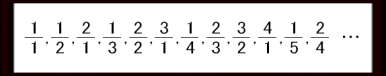
上のように規則的に数が並んでいます。値が1/2(2分の1)となる
4番目の数は前から数えて何番目の数でしょうか。
かたまりでとらえるというのをもう一歩進めると
このようになります。

分子と分母を足すわけです。
求めたいのが4/8(8分の4)ということで
分子分母を足すと12になります。12のかたまりに答えはありますよね。
2から数列が始まっていますから12というのは11番目のかたまりです。
10個目までを先ほどのように足して55で
分子は1から必ず始まるので4番目。
55+4で答えは59番目になります。
この問題に限って言えば分子分母を足さない方が
もしかしたら混乱が少ないかもしれませんが
問題をじっと見ていると「足した方がいいんじゃない?」と
言われている気がしますね。
もっとちょっと違うとらえ方も出来ます。
もう一度、問題を書きますね。
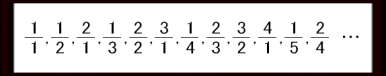
上のように規則的に数が並んでいます。値が1/2(2分の1)となる
4番目の数は前から数えて何番目の数でしょうか。
かたまりでとらえるというのをもう一歩進めると
このようになります。

分子と分母を足すわけです。
求めたいのが4/8(8分の4)ということで
分子分母を足すと12になります。12のかたまりに答えはありますよね。
2から数列が始まっていますから12というのは11番目のかたまりです。
10個目までを先ほどのように足して55で
分子は1から必ず始まるので4番目。
55+4で答えは59番目になります。
この問題に限って言えば分子分母を足さない方が
もしかしたら混乱が少ないかもしれませんが
問題をじっと見ていると「足した方がいいんじゃない?」と
言われている気がしますね。

